Levels of measurement – Nominal, Ordinal, Interval, Ratio.

In measuring, one devises some mapping rule and then translates the observation of property indicants using this rule. For each concept or construct, several types of measurement are possible; the appropriate choice depends on what you assume about the mapping rules. Each one has its own set of underlying assumptions about how the numerical symbols correspond to real-world observations.

Mapping rules have four assumptions:

1. Numbers are used to classify, group, or sort responses. No order exists.

2. Numbers are ordered. One number is greater than, less than, or equal to another number.

3. Differences between numbers are ordered. The difference between any pair of numbers is greater than,

less than, or equal to the difference between any other pair of numbers.

4. The number series has a unique origin indicated by the number zero. This is an absolute and meaningful zero point

Why is Level of Measurement Important?

First, knowing the level of measurement helps you decide how to interpret the data from that variable. When you know that a measure is nominal (like the one just described), then you know that the numerical values are just short codes for the longer names. Second, knowing the level of measurement helps you decide what statistical analysis is appropriate on the values that were assigned. If a measure is nominal, then you know that you would never average the data values or do a t-test on the data.

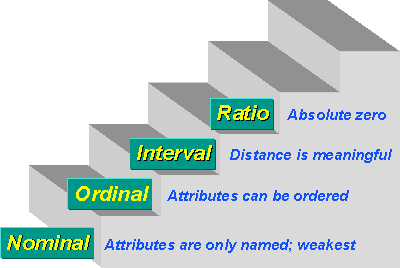
There are typically four levels of measurement that are defined:

• Nominal
• Ordinal
• Interval
• Ratio

In nominal measurement the numerical values just “name” the attribute uniquely. No ordering of the cases is implied. For example, jersey numbers in basketball are measures at the nominal level. A player with number 30 is not more of anything than a player with number 15, and is certainly not twice whatever number 15 is.

In ordinal measurement the attributes can be rank-ordered. Here, distances between attributes do not have any meaning. For example, on a survey you might code Educational Attainment as 0=less than high school; 1=some high school.; 2=high school degree; 3=some college; 4=college degree; 5=post college. In this measure, higher numbers mean more education. But is distance from 0 to 1 same as 3 to 4? Of course not. The interval between values is not interpretable in an ordinal measure.

In interval measurement the distance between attributes does have meaning. For example, when we measure temperature (in Fahrenheit), the distance from 30-40 is same as distance from 70-80. The interval between values is interpretable. Because of this, it makes sense to compute an average of an interval variable, where it doesn’t make sense to do so for ordinal scales. But note that in interval measurement ratios don’t make any sense - 80 degrees is not twice as hot as 40 degrees (although the attribute value is twice as large).

Finally, in ratio measurement there is always an absolute zero that is meaningful. This means that you can construct a meaningful fraction (or ratio) with a ratio variable. Weight is a ratio variable. In applied social research most “count” variables are ratio, for example, the number of clients in past six months. Why? Because you can have zero clients and because it is meaningful to say that “…we had twice as many clients in the past six months as we did in the previous six months.”

It’s important to recognize that there is a hierarchy implied in the level of measurement idea. At lower levels of measurement, assumptions tend to be less restrictive and data analyses tend to be less sensitive. At each level up the hierarchy, the current level includes all of the qualities of the one below it and adds something new. In general, it is desirable to have a higher level of measurement (e.g., interval or ratio) rather than a lower one (nominal or ordinal).

Importance of Measurement:

Measurement plays a crucial role in research by:

• Providing a common language: Numbers and categories allow researchers to communicate their findings clearly and concisely to others.
• Enabling data analysis: Measurement allows researchers to use statistical and other analytical tools to explore patterns, relationships, and differences in their data.
• Enhancing objectivity: By assigning numbers or labels to characteristics, researchers can minimize subjectivity and bias in their data collection and analysis.
• Facilitating generalization: Measurement allows researchers to draw conclusions about populations based on data collected from samples.

Challenges of Measurement:

However, measurement also presents several challenges:

• Choosing the right level of measurement: Selecting the appropriate level of measurement depends on the nature of the characteristics being measured and the research questions being addressed.
• Ensuring measurement reliability: Measurement should be consistent and reproducible to provide accurate data.
• Ensuring measurement validity: Measurement should actually reflect the characteristics it is intended to measure.
• Dealing with missing data: Missing data can arise due to various reasons and can complicate data analysis.

 Source: https://conjointly.com/kb/levels-of-measurement/