The Logic of Hypothesis Testing As just stated, the logic of hypothesis testing in statistics involves four steps.
- State the Hypothesis: We state a hypothesis (guess) about a population. Usually the hypothesis concerns the value of a population parameter.
- Define the Decision Method: We define a method to make a decision about the hypothesis. The method involves sample data.
- Gather Data: We obtain a random sample from the population.
- Make a Decision: We compare the sample data with the hypothesis about the population. Usually we compare the value of a statistic computed from the sample data with the hypothesized value of the population parameter.
If the data are consistent with the hypothesis we conclude that the hypothesis is reasonable. NOTE: We do not conclude it is right, but reasonable! AND: We actually do this by rejecting the opposite hypothesis (called the NULL hypothesis). More on this later.
If there is a big discrepancy between the data and the hypothesis we conclude that the hypothesis was wrong.
1. First Step: State the Hypothesis
- Stating the hypothesis actually involves stating two
opposing hypotheses about the value of a population
parameter.
- The Null Hypothesis (Ho). This hypothesis
states that the treatment has no effect. For
our example, we formally state:
The null hypothesis (Ho) is that prenatal exposure to alcohol has no effect on the birth weight for the population of lab rats. The birthweight will be equal to 18 grams. This is denoted
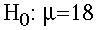
- The Alternative Hypothesis (H1). This hypothesis
states that the treatment does have an effect.
For our example, we formally state:
The alternative hypothesis (H1) is that prenatal exposure to alcohol has an effect on the birth weight for the population of lab rats. The birthweight will be different than 18 grams. This is denoted
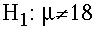
Example: Suppose we have are interested in the effect of prenatal exposure of alcohol on the birth weight of rats. Also, suppose that we know that the mean birth weight of the population of untreated lab rats is 18 grams.
Here are the two opposing hypotheses:
2. Second Step: Define the Decision Method
- We must define a method that lets us decide whether the
sample mean is different from the hypothesized population
mean. The method will let us conclude whether (reject
null hypothesis) or not (accept null hypothesis) the treatment
(prenatal alcohol) has an effect (on birth weight).
We will go into details later. 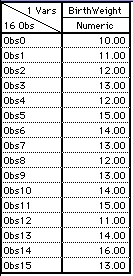
3. Third Step: Gather Data.
- Now we gather data. We do this by obtaining
a random sample from the population.
Example: A random sample of rats receives daily doses of alcohol during pregnancy. At birth, we measure the weight of the sample of newborn rats. The weights, in grams, are shown in the table.
We calculate the mean birth weight.
Experiment 1 Sample Mean = 13
4. Fourth Step: Make a Decision
- We make a decision about whether the mean of the sample
is consistent with our null hypothesis about the population
mean.
- If the data are consistent with the null hypothesis
we conclude that the null hypothesis is reasonable.
Formally: we do not reject the null hypothesis.
- If there is a big discrepency between the data and
the null hypothesis we conclude that the null hypothesis
was wrong.
Formally: we reject the null hypothesis.
- If a sample of rat pups which were exposed to prenatal
alcohol has a birth weight "near" 18 grams we conclude
that the treatement does not have an effect.
Formally: We do not reject the null hypothesis that prenatal exposure to alcohol has no effect on the birth weight for the population of lab rats.
- If our sample of rat pups has a birth weight "far"
from 18 grams we conclude that the treatement does
have an effect.
Formally: We reject the null hypothesis that prenatal exposure to alcohol has no effect on the birth weight for the population of lab rats.
Example: We compare the observed mean birth weight with the hypothesized value, under the null hypothesis, of 18 grams.
Formally: We reject the null hypothesis that prenatal exposure to alcohol has no effect on the birth weight for the population of lab rats.